数据结构第二讲课程笔记——线性表

nets:[[../else/数据结构]] 课程笔记

2.1 线性表的类型定义

线性表是一种最简单的线性结构

线性结构的基本特征为：

线性结构是一个数据元素的有序（次序）集

1. 集合中必存在唯一的一个“第一元素”；
2. 集合中必存在唯一的一个“最后元素”；
3. 除最后元素在外，均有唯一的后继；
4. 除第一个元素以外，均有唯一的前驱；

抽象数据类型线性表的定义如下：

ADT List{
数据对象：
D={a(i)|a(i)属于ElemSet,i=1,2,...,n,n>0}
{称n为线性表的表长；称n=0时的线性表为空表。}
数据关系：
R1={<a(i-1),a(i)>a(i-1),a∈D,i=2,...,n}
{设线性表为(a1,a2,.，ai,...an),称i为a:在线性表中的位序。}
基本操作：
结构初始化操作
	InitList(&L)
	操作结果：
	构造一个空的线性表L。
结构销毁操作
	DestroyList(&L)
	初始条件：线性表L已存在。
	操作结果：销毁线性表L。
引用型操作
加工型操作
}ADT List

引用性操作

ListEmpty(L)
(线性表判空)
初始条件：线性表L已存在。
操作结果：若L为空表，则返回TRUE,否则FALSE。

ListLength(L)
(求线性表的长度)
初始条件：线性表L已存在。
操作结果：返回L中元素个数。

PriorElem(L,cur_e,&pre_e)
(求数据元素的前驱)》
初始条件：线性表L已存在。
操作结果：若cur_e是L的元素，但不是第一个，则用pre_e返回它的前驱，否则操作失败，pre_e无定义。

NextElem(L,cur e,&next e)
(求数据元素的后继)
初始条件：线性表L已存在。
操作结果：若cur_e是L的元素，但不是最后一个，则用
next_e返回它的后继，否则操作失败，next_e无定义。

GetElem(L,i,&e)
(求线性表中某个数据元素)
初始条件：线性表L已存在，且1<=i<=LengthList(L)
操作结果：用e返回L中第i个元素的值。

LocateElem(L,e,compare())
(定位函数)
初始条件：线性表L已存在，e为给定值，compare()是元素判定函数。
操作结果：返回L中第l个与e满足关系compare()的元素的位序。若这样的元素不存在，则返回值为0。

ListTraverse(L,visit())
（遍历线性表)
初始条件：线性表L已存在，Visit()为某个访问函数。
操作结果：依次对L的每个元素调用函数visit()。一旦visit()失败，则操作失败。

加工型操作

ClearList(&L)
(线性表置空)
初始条件：线性表L已存在。
操作结果：将L重置为空表。

PutElem(&L,i,&e)
(改变数据元素的值)
初始条件：线性表L已存在，且1≤i≤LengthList(L)。
操作结果：L中第i个元素赋值同的值。

ListInsert(&L,i,e)
(插入数据元素)
初始条件：线性表L已存在，且1≤i≤LengthList(L)+1
操作结果：在L的第i个元素之前插入新的元素e,L的长
度增1。

ListDelete(&L,i,&e)
(删除数据元素)
初始条件：线性表L已存在且非空，1≤i≤LengthList(L)。
操作结果：删除L的第i个元素，并用返回其值，L的长度减1。

例题

例2-1假设：有两个集合A和B分别用两个线性表LA和LB表
示，即：线性表中的数据元素即为集合中的成员。
现要求一个新的集合A=AUB。

void union(List &La,List Lb)
La_len=ListLength(La);//求线性表的长度
Lb_len ListLength(Lb);
for (i=1;i<=Lb len;++)
	GetElem(Lb,i,e);//取Lb中第i个数据元素赋给e
	if (!LocateElem(La,e,equal()))
		ListInsert(La,++La len,e);
//La中不存在和e相同的数据元素，则插入之
}//union

例2-2已知一个非纯集合B,试构造一个纯集合A,使A中只包含B中所有值各不相同的数据元素。

void union(List &La,List Lb){
InitList(La);∥构造（空的）线性表LA
La len=ListLength(La);
Lb len=ListLength(Lb);
for (i=1;i<=Lb len;i++){
	GetElem(Lb,i,e);/∥取Lb中第i个数据元素赋给e
	if (!LocateElem(La,e,equal()))
		ListInsert(La,++La len,e);
	}∥La中不存在和e相同的数据元素，则插入之
}//union

若线性表中的数据元素相互之间可以比较，并且数
据元素在线性表中依值非递减或非递增有序排列，
即a:≥a-1或a:≤a-1(i=2,3,,n),则称该线性表为有序表(Ordered List)。

void purge(List &La,List Lb){
InitList(La);
La len=ListLength(La);
Lb len=ListLength(Lb);∥求线性表的长度
for (i=1;i<=Lb len;i++){
	GetElem(Lb,i,e);∥取Lb中第i个数据元素赋给e
	if (ListEmpty(La)l‖！equal(en,e){
		ListInsert(La,++La len,e);
		en=e,
		}∥La中不存在和e相同的数据元素，则插入之
	}
}//purge

2.2 顺序表的表示和实现

顺序映象
——以x的存储位置和y的存储位置之间某种关系表示逻辑关系<x,y>。

最简单的一种顺序映象方法是：
令y的存储位置和X的存储位置相邻。

#define LIST INIT SIZE 80  //线性表存储空间的初始分配量
#define LISTINCREMENT 10  //线性表存储空间的分配增量
typedef struct{
ElemType*elem;   //存储空间基址
int length;  //当前长度
int listsize;  //当前分配的存储容量（sizeof(ElemType)为单位
}SqList; // 俗称顺序表

线性表的基本操作在顺序表中的实现
InitList(&L)//结构初始化

Status InitList_Sq(SqList&L){//构造一个空的线性表
L.elem (ElemType*)malloc (LIST_INIT_SIZE*sizeof(ElemType);
if (!L.elem)exit(OVERFLOW);
L.length=0;
L.listsize LIST INIT SIZE
return OK;
}//InitList Sq

					算法时间复杂度：O(1)

LocateElem(L,e,compare())//查找

int LocateElem_Sq(SqList L,ElemType e,
Status (*compare)(ElemType,ElemType)){
//在顺序表中查询第一个满足判定条件的数据元素，
//若存在，则返回它的位序，否则返回0
i=1; //i的初值为第1元素的位序
p=L.elem; //p的初值为第1元素的存储位量
while (i<=L.length &&!(*compare)(*p++,e))++i;
if (i<=L.length)return i;
else return 0;
}/∥LocateElem Sq

算法的时间复杂度为：
O(ListLength(L))

ListInsert(&L,i,e)//插入元素

Status ListInsert Sq(SqList &L,int i,ElemType e){
/∥在顺序表L的第个元素之前插入新的元素，
/∥i的合法范围为l≤i≤L.length+l
if (i<1||i>L.length+1)return ERROR; //插入位置不合法
if (L.length >=L.listsize){ //当前存储空间已满，增加分配
newbase=(ElemType *)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof (ElemType));
if(!newbase)exit(OVERFLOW);//存储分配失败
L.elem=newbase; //新基址
L.listsize+=LISTINCREMENT;//增加存储容量
q=&(L.elem[i-l]) //q指示插入位置
for (p=&(L.elem[L.length-1]);p>=q;--p)
*(p+1)=*p; //插入位置及之后的元素右移
*q=e;//插入e
++L.length;//表长增1
return OK;
O(ListLength(L))
}//ListInsert Sq 
时间复杂度：O（L）

ListDelete(&L,i)//删除元素

Status ListDelete_Sq(SqList &L,int i,ElemType &e){
if ((i<1)||(i>L.length))return ERROR;//删除位置不合
p=&(L.elem[i-l]);//p为被删除元素的位置
e=*p;//被删除元素的值赋给e
q=L.elem+L.length-l;//表尾元秦的位置
for (++p;p<=q;++p)*(p-1)=*p;//元素左移
//被删除元素之后的元素左移
--L.length;
//表长减1
return OK;
}//ListDelete Sq
算法时间复杂度为
O(ListLength(L)）

2.3 链表的表示和实现

一、单链表

用一组地址任意的存储单元存放线性表中的数据元素。

以元素（数据元素的映象）+指针（指示后继元素存储置）=结点(表示数据元素或数据元素的映象)

以“结点的序列”表示线性表称作链表以线性表中第一个数据元素的存储地址作为线性表的地址，称作线性表的头指针。

有时为了操作方便，在第一个结点之前虚加一个“头结点”，
以指向头结点的指针为链表的头指针。

二、结点和单链表的C语言描述

Typedef struct LNode{
ElemType data;//数据域
struct Lnode *next;//指针域
}LNode,*LinkList;
LinkList L;∥L为单链表的头指针

三、单链表操作的实现

GetElem(L,i,e) ; //取第i个数据元素

Status GetElem_L(LinkList L,int i,ElemType &e)
//L是带头结点的链表的头指针，以e返回第i个元素
p=L->next;j=1;//p指向第一个结点，j为计数器
while (p &&j<i){p=p->next;++j;}
//顺指针向后查找，直到p指向第i个元素或p为空
if (!p||j<i) return ERROR;//第i个元素不存在
e =p->data;//取得第i个元素
return OK;
}//GetElem L
算法时间复杂度为：
O(ListLength(L))

ListInsert(&L,i,e)//插入数据元素

Status ListInsert_L(LinkList L,int i,ElemType e){
Elemtype *p;
p=L;
for(int j=0;j<i-1;j++){
	p=p->next;
	}
	if(!p||j>i-1) return ERROR;
	Lnode*s;
	s=new Lnode;
	s->data=e;
	s->next=p->next;
	p->next=s;
	return OK;
}

ListDelete(&L,i,e)//删除数据元素

Status ListDelete_L(LinkList L,int i,ElemType &e){
Lnode *p,*q;
p=L;
for(int j=0;j<i-1;j++){
	p=p->next;
	}
if(!(p->next)||j>i-1) return 0;
q=p->next;
p->next=q->next;
e=q->data;//e用来存删除的数据
free(q);
}

ClearList(&L)//重置线性表为空表

void ClearList(&L){
Lnode *p,*q;
p=L;
whlie(L->next!=NULL){
	p=L->next;
	L->next=p->next;
	free(p);
	}
}

CreateList(&L,n)//生成含n个数据元素的链表

void CreateList L(LinkList &L,int n){
//逆序输入n个数据元素，建立带头结点的单链表
L=(LinkList)malloc (sizeof (LNode));
L->next=NULL;//先建立一个带头结点的单链表
for (i=n;i>0;--1){
p=(LinkList)malloc (sizeof (LNode));
scanf(&p->data);//输入元素值
p->next=L->next;L->next=p;//插入
//
}//CreateList L
算法的时间复杂度为：
O(Listlength(L))

例题

合并有序链表La，Lb到Lc中。

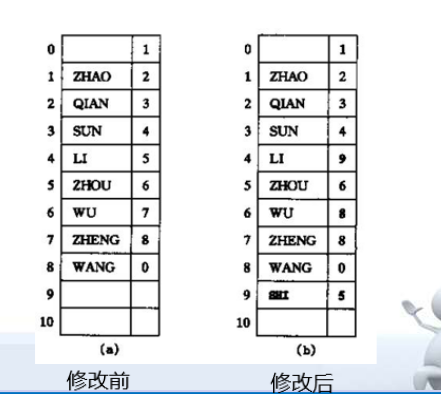
四、其他形式的链表

1. 静态链表

typedef struct{
ElemType data;
//下一个结点的数组序号
int next;
}Node;
typedef struct{
Node*nodes;
int len;
int size;
}LinkList;

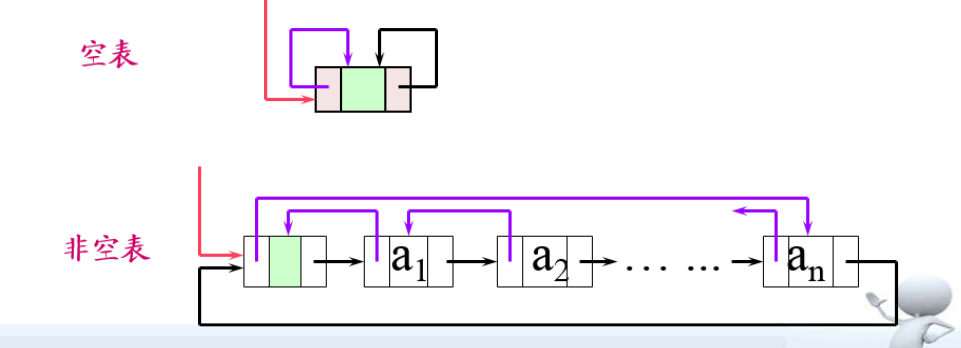
2. 循环链表

3. 双向链表（不管了）

typedef struct DuLNode{
ElemType data;//数据域
struct DuLNode *prior;//指向前驱的指针域
struct DuLNode *next://指向后继的指针域
}DuLNode,*DuLinkList;

双向链表的操作特点：
“查询”和单链表相同。
“插入”和“删除”时需要同时修改两个方向上的指针。

六、有序表类型

抽象数据类型

LocateElem(L,e,&q,int(*compare)(ElemType,ElemType))
初始条件：有序表L已存在。
操作结果：若有序表L中存在元素，则q指示L中第一个值为e的元素的位置，并返回函数值TRUE;否则q指示第一个大于e的元素的前驱的位置，并返回函数值FALSE。

2.4 线性表应用举例

一元多项式相加（弱化了）

基本操作：
CreatPolyn (&P,m)
操作结果：输入m项的系数和指数，建立一元多项式P。
DestroyPolyn (&P)
初始条件：一元多项式P已存在。
操作结果：销毁一元多项式P。
PrintPolyn (&P)
初始条件：一元多项式P已存在。
操作结果：打印输出一元多项式P。
PolynLength(P)
初始条件：一元多项式P已存在。
操作结果：返回一元多项式P中的项数。
AddPolyn &Pa,&Pb
初始条件：一元多项式Pa和Pb已存在。
操作结果：完成多项式相加运算，即：Pa=Pa+Pb,并销毁一元多项式Pb。
SubtractPolyn (&Pa,&Pb）
……

重难点

• 单链表删除结点/插入新节点。

---

References