nets:[[../else/数据结构]] 课程笔记

3.1 栈的定义、表现及实现（重点）

一、栈的类型定义

栈(stack)是限定仅在表尾进行插入或删除操作的线性表。因此，对栈来说，表尾端有其特殊意义，称为栈顶，相应地，表头端称为栈底。不含元素的空表称为空栈。

假设S=（al,a2,.an),则称al为栈底元素，an为栈顶元素。栈中元素按照al,a2,..an的次序进栈，按照an,,a2,al的次序出栈，因此，栈又称后进先出的线性表。

基本操作：
InitStack(&S)
操作结果：构造一个空栈S

DestroyStack(&S)
初始条件：栈S已存在。
操作结杲：栈S被销毁。

StackEmpty(S)
初始条件：栈S已存在。
操作结果：若栈S为空栈，则返回TRUE,否则FALSE。

StackLength(S)
初始条件：栈S已存在。
操作结杲：返回S的元素个数，即栈的长度。

GetTop(S,&e)
初始条件：栈S已存在且非空。操作结果：用e返回S的栈顶元素。

ClearStack(&S)
初始条件：栈S已存在。
操作结果：将S清为空栈。

Push(&S,e)
初始条件：栈S已存在。
操作结果：插入元素e为新的栈顶元素。

pop(&S,&e) //出栈

StackTravers(&S,visit)//遍历

二、栈的实现

1. 顺序栈

栈的顺序储存表示

#define STACK INIT SIZE 100:
#define STACKINCREMENT 10:
typedef struct{
SElemType *base;//分配空间
SElemType *top; //指向栈顶空处
int stacksize;
}SqStack;

初始化

Status InitStack (SqStack &S)
{//构造一个空栈S
S.base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(ElemType));
if(!S.base)exit(OVERFLOW);//存储分配失败
S.top=S.base;
S.stacksize STACK_INIT_SIZE;
return OK;
}

进栈

Status Push(SqStack &S,SElemType e){
	if(S.top-S.base>=S.stacksize){
		S.base=(SELemType*)Realloc(S.stacksize+STACKINCREMENT)*sizeof(ElemType));
		if(!S.base)exit(OVERFLOW);
		S.top=S.base+S.stacksize;
		S.stacksize+=STACKINCREMENT;
	}
	*S.top++=e;
}

出栈

Status Pop(SqStack &S,SElemType &e){
	if(S.top=S.base)return 0;
	e=--*S.top;//e为出栈元素
	return 1;
}

2. 链栈

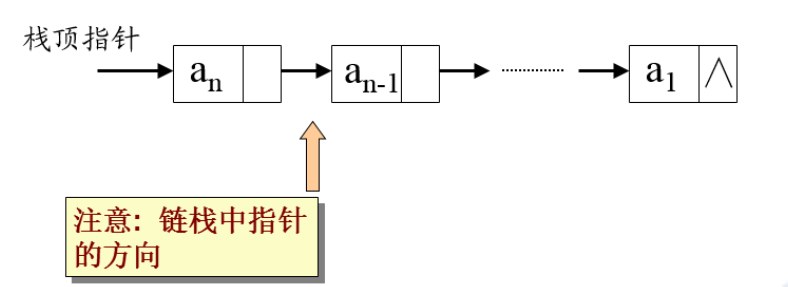
3.2 栈的应用举例（考小题）

一、数制转换

算法基于原理：
N=(N div d) x d + N mod d
例如：（1348)10=(2504)8，其运算过程如下：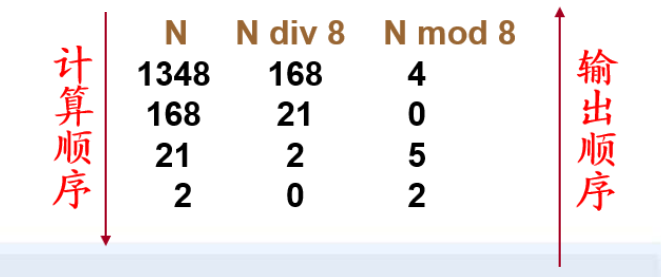

二、括号匹配的检验

例二、括号匹配的检验
假设在表达式中
()或[([][])]
等为正确的格式，
[(])或([())或(()])
均为不正确的格式。
则检验括号是否匹配的方法可用
“期待的急迫程度”这个概念来描述。

算法的设计思想：
1)凡出现左括孤，则进栈；
2)凡出现右括孤，首先检查栈是否空。若栈空，则表明该“右指孤”多余，否则和栈顶元素比较，若相匹配，则“左括孤出栈”，否则表明不匹配。
3)表达式检验结束时，若栈空，则表明表达式中匹配正确，
否则表明“左括孤”有余。

三、行编辑程序问题

在用户输入一行的过程中，允许用户输入出差错，并在发现有误时可以及时更正。

合理的作法是：
设立一个输入缓冲区，用以接受用户输入的一行字符，然后逐行存入用户数据区，并假设“#”为退格符，“@”为退行符。

假设从终端接受了这样两行字符：
whli#ilr#e（s#*s)
outcha@putchar(*s-#++);
则实际有效的是下列两行：
while (*s)
putchar(*s++);

四、迷宫求解

设定当前位置的初值为人口位置：
do{
若当前位置可通，
则{将当前位置插入栈顶， //纳人路径
若该位置是出口位置，则结束； //求得路径存放在栈中
否则切换当前位置的东邻方块为新的当前位置：
}
否则，
若栈不空且栈顶位置尚有其他方向未经探索，
则设定新的当前位置为沿顺时针方向旋转找到的栈顶位置的下一相邻块：
若栈不空但栈顶位置的四周均不可通，
则{删去栈顶位置； //从路径中删去该通道块
若栈不空，则重新测试新的栈顶位置，
直至找到一个可通的相邻块或出栈至栈空：
}
}while(栈不空)；

五、表达式求值(要弄懂)

例如：Exp=a×b+(c-d/e)×f
前缀式：+×ab-c/def
中缀式：a×b+c-d/exf
后缀式：abxcde/-fx+
结论：1)操作数之间的相对次序不变；
2)运算符的相对次序不同；

3.3 队列的定义、表示及实现

一、队列的类型定义

队列(queue)在计算机科学中，是一种先进先出的线性表。它只允许在表的前端（front)进行删除操作，而在表的后端(rear)进行插入操作。
进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

基本操作：
InitQueue(&Q)
操作结果：构造一个空队列
DestroyQueue(&Q)
初始条件：队列Q已存在
操作结果：队列Q被销毁，不在存在；
QueueEmpty(Q)
初始条件：队列Q已存在
操作结果：若为空队列，则返回TURE，否则返回FALSE。
QueueLength(Q)
初始条件：队列Q已存在
操作结果：返回Q的元素个数，即队列长度
GetHead(Q,&e)
初始条件：Q为非空队列
操作结果：用e返回Q的队头元素
ClearQueue(&Q)
初始条件：队列Q已存在
操作结果：将Q清为空队列
EnQueue(&Q,e)
初始条件：队列Q已存在
操作结果：插入元素e为Q的新的队尾元素
DeQueue(&Q,&e)
初始条件：Q为非空队列
操作结果：删除Q的队头元素，并用e返回其值；
QueueTravers(Q,visitO)
遍历

二、队列类型的实现

1. 链队列——链式映像

typedef struct QNode{//结点类型
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct{//链队列类型
QueuePtr front;//队头指针
QueuePtr rear;//队尾指针
}LinkQueue;

Status InitQueue (LinkQueue &Q){//构造一个空队列Q
Q.front=Q.rear=(QueuePtr)malloc(sizeof(QNode));
if (!Q.front)exit (OVERFLOW);//存储分配失败
Q.front->next=NULL;
return OK;
}

Status EnQueue(LinkQueue &Q，QElemType e){
p=(QueuePrt)malloc(sizeof(QNode));
if(!p)exit(OVERFLOW);
p.data=e; p->next=NULL;
Q.rear->next=p; Q.rear=p;
return OK;
}

Status DeQueue (LinkQueue &Q,QElemType &e){
//若队列不空，则删除Q的队头元素，
//用e返回其值，并返回OK;否则返回ERROR
if (Q.front ==Q.rear) return ERROR:
p =Q.front->next; e=p->data;
Q.front->next=p->next;
if (Q.rear ==p)Q.rear=Q.front;
free (p);
return OK:
}

2. 循环队列——顺序映像

#define MAXQSIZE 100//最大队列长度
typedef struct
QElemType*base;//动态分配存储空间
int front;//头指针，若队列不空，指向队列头元素
int rear;//尾指针，若队列不空，指向队列尾元素的下一个位置
}SqQueue;

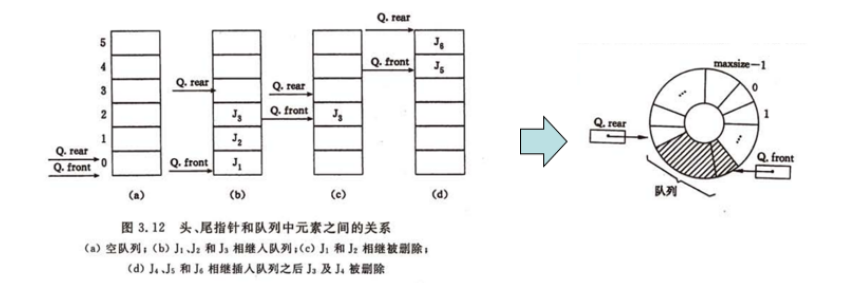
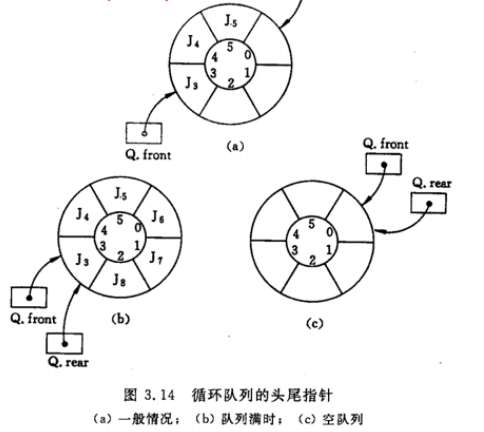
为此，为了区分队列为”满”与队列为“空”，有两种方法：1、设置标志位区分队列满还是空状态；
2、少用一个元素空间，约定以“队列头指针在队尾的下一位置上”作为队列呈“满”状态的标志。

Status InitQueue (SqQueue &Q){
//构造一个空队列Q
Q.base =(QElemType *malloc(MAXQSIZE *sizeof (ElemType));
if(!Q.base)exit(OVERFLOW);//存储分配失败
Q.front=Q.rear =0;
return OK;}

Status EnQueue (SqQueue &Q,ElemType e){
//插入元素e为Q的新的队尾元素
if ((Q.rear+1)%MAXQSIZE==Q.front)
return ERrOR;//队列满
Q.base [Q.rear]=e;
Q.rear =(Q.rear+1)%MAXQSIZE;
return OK;}

Status DeQueue (SqQueue &Q,ElemType &e){
//若队列不空，则删除Q的队头元素，
//用e返回其值，并返回OK;否则返回ERROR
if (Q.front ==Q.rear)return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;}

3.4 队列的应用举例

例1：假设一字符串存入一队列中，设计算法将该字符串置逆存放。
解题分析
可以使用一个辅助栈，将队列中的元素送入栈中，再从栈中送回队列中。

例2: 假设单链表中的数据元素是字符串。设计算法利用栈和队列判别链表中的字符串是否回文序列，是则返回1，否则返回0。如“abcba”是回文，而“abab不是回文。
解题分析
这是一个判断字符串是否中心对称问题。扫描链表，同时将数据入队和入栈，再将出队和出栈的元素比较，若全部相同
则是回文。

栈与递归

汉诺塔问题

汉诺塔的递归解决方法（分治法）
分3步

把前n-1个盘子移到中间的塔座B。
把最后一个盘子移到塔座C
把中间塔座B上的n-1个盘子移动塔座C
方法可行吗？

八皇后问题（回溯法）

八皇后问题是十九世纪著名的数学家高斯提出的：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻（任意两个皇后都不能处于同一行、同一列或同一斜线上)，问有多少种摆法。

数据结构第三讲课程笔记——栈和队列