数据结构第五讲课程笔记——树和二叉树

nets:[[../else/数据结构]] 课程笔记

5.1 树的类型定义

数据对象D:

D是具有相同特性的数据元素的集合。

数据关系R:

若D为空集，则称为空树。
否则：(1)在D中存在唯一的称为根的数据元素root;
(2)当n>1时，其余结，点可分为m(m>0)个互不相交的有限集T1,T2,….,Tm,其中每一棵子集本身又是一棵符合本定义的树，称为根root的子树。

基本操作：

查找类

Root(T)//求树的根结点
Value(T,cur_e)//求当前结点的元素值
Parent(T,cur_e)//求当前结点的双亲结点
LeftChild(T,cur_e)//求当前结，点的最左孩子
RightSibling(T,cur_e)//求当前结点的右兄弟
TreeEmpty(T)//判定树是否为空树
TreeDepth(T)//求树的深度
TraverseTree(T,Visit())//遍历

插入类

InitTree(&T)//初始化置空树
CreateTree(&T,definition)//按定义构造树
Assign(T,cur_e,value)//给当前结点赋值
InsertChild(&T,&p,i,c)//将以c为根的树插入为结点p的第i棵子树

删除类

ClearTree(&T)//将树清空
Destroy Tree(&T)//销毁树的结构
DeleteChild(&T,&p,i)//删除结点p的第棵子树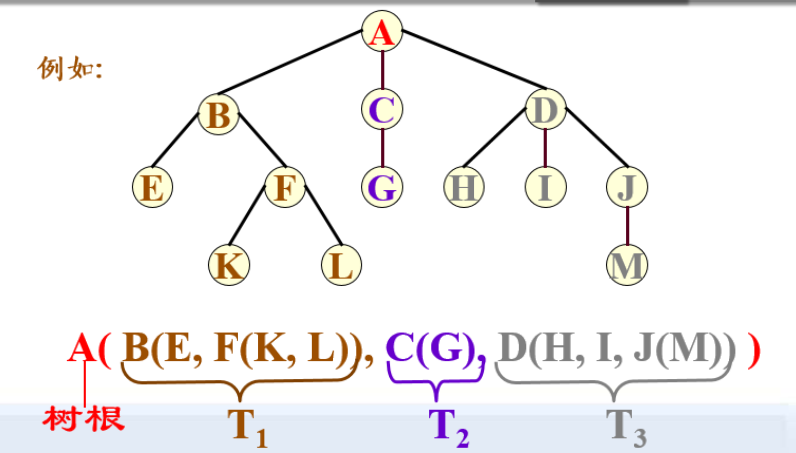

相关概念

有向树：

(1)有确定的根；
(2)树根和子树根之间为有向关系

有序树：

子树之间存在确定的次序关系。

无序树：

子树之间不存在确定的次序关系。

树形结构和线性结构的特点

线性结构

第一个数据元素（无前驱）
最后一个数据元素（无后继）
其它数据元素
(一个前驱、一个后继)

树形结构

根节点(无前驱)
多个叶子节点(无前驱后继)
其它数据元素(一个前驱、多个后继)

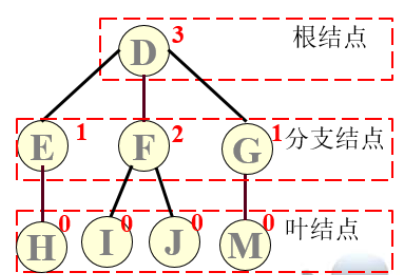
结点：数据元素+若干指向子树的分支
结点的度：分支的个数
树的度：树中所有结点的度的最大值
叶子结点：度为零的结点
分支结点：度大于零的结点
结点的层次：假设根结点的层次为1，第1层的结点的子树根结点的层次为l+1
树的深度：树中叶子结点所在的最大层次
(从根到结，点的)路径：由从根到该结点所经分支和结，点构成
孩子结点、双亲结点
兄弟结点、堂兄弟
祖先结点、子孙结点

森林：是m(m≥0)棵互不相交的树的集合。
任何一棵非空树是一个二元组
Tree=(root,F)
其中：root被称为根结点；F被称为子树森林；

5.2 二叉树的类型定义

二叉树或为空树，或是由一个根结点加上两棵分别称为左子树和不子树的、互不交的二叉树组成。

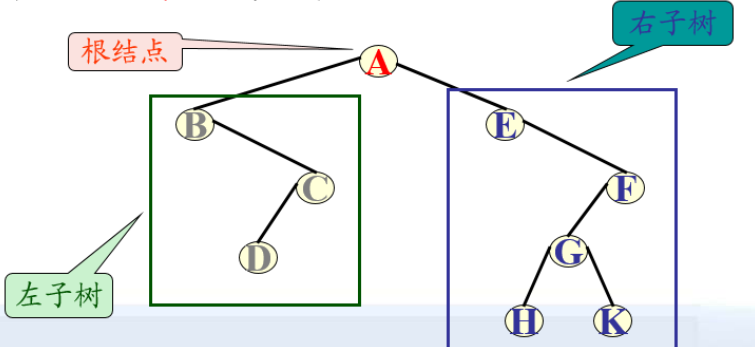
二叉树的五种基本形态

空树、只含根节点、右子树为空树、左子树为空树、左右子树均不为空树。
满二叉树：指的是深度为k且含有2**k-1个结点的二叉树。
完全二叉树：树中所含的n个结点和满二叉树中编号为1至n的结点一一对应。

二叉树的主要的基本操作

查找类

Root(T);
Value(T,e);
Parent(T,e);
LeftChild(T,e);
RightChild(T,e);
LeftSibling(T,e);
RightSibling(T,e);
BiTreeEmpty(T);
BiTreeDepth(T);
PreOrderTraverse(T,Visit());
InOrderTraverse(T,Visit());
PostOrderTraverse(T,Visit());
LevelOrderTraverse(T,Visit());

插入类

InitBiTree(&T);
Assign(T,&e,value);
CreateBiTree(&T,definition);
InsertChild(T,p,LR,c);

删除类

ClearBiTree(&T);
DestroyBiTree(&T);
DeleteChild(T,p,LR);

二叉树的重要特性

性质1：在二叉树的第i层上至多有2**(i-1)个结点 (i>=1)
性质2：深度为k的二叉树上至多含2**i-1个结，点（k≥1)
性质3：对任何一棵二叉树，若它含有n0个叶子结点、n2个度为2的结点，则必存在关系式：n0=n2+1。
结点总数n=n0+n1+n2
分支总数n=n1+2*n2
性质4：具有n个结，点的完全二叉树的深度为(log2n)+1
性质5：若对含n个结点的完全二叉树从上到下且从左至右进行1至n的编号，则对完全二叉树中任意一个编号为i的结点：
(1)若i=1，则该结点是二叉树的根，无双亲，否则，编号为i/2的结点为其双亲结点；
(2)若2i>n，则该结点无左孩子，否则，编号为2i的结点为其左孩子结点；
(3)若2i+1>n，则该结点无右孩子结点，否则，编号为2i+1的结点为其右孩子结点。

5.3 二叉树的储存结构

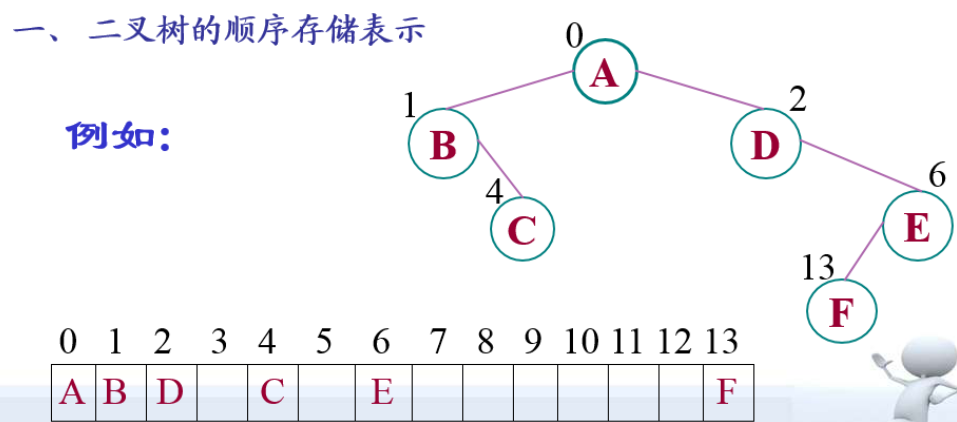
一、二叉树的顺序存储表示

#define MAX_TREE_SIZE 100//二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE];//0号单元存储根结点
SqBiTree bt;

二、二叉树的链式存储表示

1. 二叉链表

typedef struct BiTNode{//结点结构
TElemType data;
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

2. 三叉链表

typedef struct TriTNode{//结点结构
TElemType data;
struct TriTNode *lchild,*rchild;//左右孩子指针
struct TriTNode*parent;//双亲指针
}TriTNode,*TriTree;

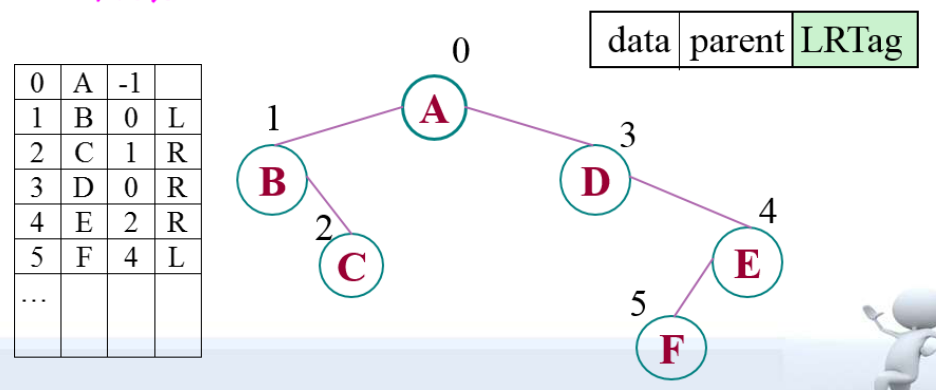
3. 双亲链表

typedef struct BPTNode{//结点结构
TElemType data;
int *parent;//指向双亲的指针
char LRTag;//左、右孩子标志域
}BPTNode
ypedef struct BPTree{//树结构
BPTNode nodes [MAX_TREE_SIZE];
int num_node;//结点数目
int root;//根结点的位置
}BPTree

4. 线索链表

（见5.5）

5.4 二叉树的遍历

一、问题的提出

顺着某一条搜索路径巡访二叉树中的结点，使得每个结点均被访问一次，而且仅被访问一次。
“访问”的含义可以很广，如：输出结点的信息等。

对“二叉树”而言，可以有三条搜索路径：

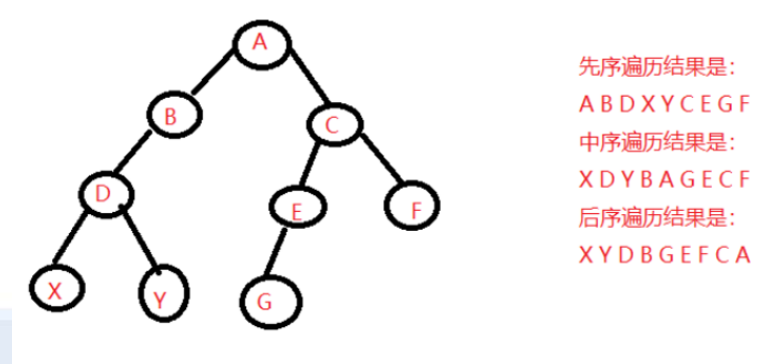
1.先上后下的按层次遍历；”先序遍历算法”
2.先左（子树）后右（子树）的遍历；“中序遍历算法”
3.先右（子树)后左（子树）的遍历。“后序遍历算法”

二、算法的递归描述

void preorder(BiTree T,void(*visit)(TElemtType&e)){
	if(T){
		visit(T->data);
		preorder(T->lchild,visit);
		preorder(T->rchild,visit);
	}
}//先序遍历

void inorder(BiTree T, void(*visit)(TElemType&e)){
	//中序遍历
	if(T){
		inorder(T->lchild,visit);
		visit(T->data);
		inorder(T->rchild,visit);
	}
}

void postorder(Bitree T,void(*visit)(TElemType&e)){
	//后序遍历
	if(T){
		postorder(T->rchild,visit);
		postorder(T->lchild,visit);
		visit(T->data);
	}
}

三、中序遍历算法的非递归描述

void inorder(BiTree T,void(*visit)(TElemType &e)){
	Stack *S;
	t=GoFarLeft(T,S);//找的最左下的结点
	while(t){
		visit(t->data);
		if(t->rchild){
			t=GoFarLeft(t->rchild,S);
		}
		else if(!StackEmpty(S)) t=pop(S);
		else t=NULL;//栈空时表明遍历结束
	}
}

BiTNode *GoFarLeft(BiTree T,Stack *S){
	if(!T) return NULL;
	while(T->lchild){
		push(S,T);
		T=T->lchild;
	}
	return T;
}

四、遍历算法的应用举例

层次遍历二叉树

层次遍历二叉树，是从根结点开始遍历，按层次次序“自上而下，从左至右”访问树中的各结点。
为保证是按层次遍历，必须设置一个队列，初始化时为空。
设T是指向根结点的指针变量，层次遍历非递归算法是：
若二叉树为空，则返回；否则，令p=T,p入队：
(1)队首元素出队到p;
(2)访问p所指向的结点：
(3)将所指向的结点的左、右子结点依次入队。直到队空为止。

#define MAX_NODE 50
void LevelorderTraverse(BTNode *T){
BTNode *Queue[MAX_NODE],*p=T;
int front=0,rear=0;
if (p!=NULL){
	Queue[++rear]=p;/*根结点入队*/
	while (front<rear){
		p=Queue[++front];visit(p->data )
		if (p->Lchild!=NULL)
			Queue[++rear]=p;/*左结点入队*/
		if (p->Rchild!=NULL)
			Queue[++rear]=p;/*右结点入队*/
		}
	}
}

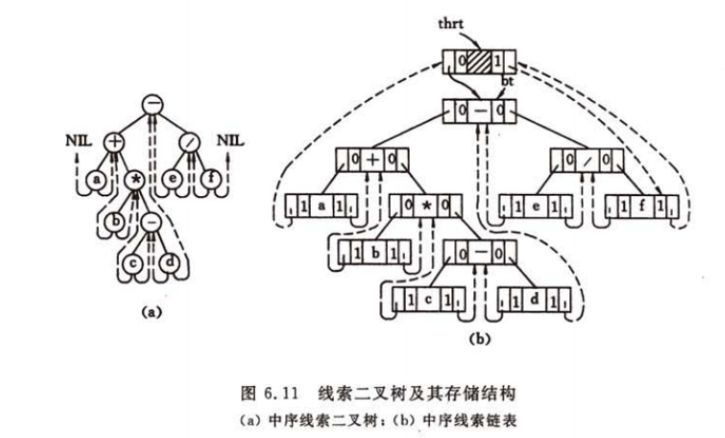
5.5 线索二叉树

一、何为线索二叉树

遍历二叉树的结果是，求得结点的一个线性序列。指向该线性序列中的“前驱”和“后继”的指针，称作“线索“。

包含”线索“的储存结构，称作”线索链表“。
与其相对应的二叉树，称作”线索二叉树“。

对线索链表中结点的约定：
在二又链表的结点中增加两个标志域，并作如下规定：
若该结点的左子树不空，则Lchild域的指针指向其左子树，且左标志域的值为”指针Link”;
否则，Lchild域的指针指向其”前驱”，且左标志的值为”线索
Thread”。
若该结点的右子树不空，则rchild域的指针指向其右子树，且右标志域的值为“指针Link”;
否则，rchild域的指针指向其“后继”，且右标志的值为“线索Thread”
如此定义的二叉树的存储结构称作“线索链表”。

typedef enum {Link,Thread} PointerThr;
//Link==0:指针，Thread-==l:线索
typedef struct BiThrNod{
TElemType data;
struct BiThrNode *lchild, *rchild;//左右指针
PointerThr LTag,RTag;//左右标志
}BiThrNode,*BiThrTree;

二、线索链表的遍历算法

由于在线索链表中添加了遍历中得到的“前驱”和“后继”的信息，从而简化了遍历的算法。

for (p=firstNode(T);p;p Succ(p))
Visit (p);
例如：对中序线索化链表的遍历算法

• 必中序遍历的第一个结点？
  左子树上处于“最左下”（没有左子树）的结点。
  中序线索链表查找前驱
• 必在中序线索化链表中结点的后继？
  若无右子树，则为后继线索所指结点；否则为对
  其右子树进行中序遍历时访问的第一个结点。中序线索链表查找后继。

void InOrder Traverse Thr(BiThr Tree T,void (*Visit)(TElemType e)){
	p=T->lchild; //p指向根结点
	while(p!=T){//空树或遍历结束时，p=T
	while(p->LTag=Link)p=p->lchild;//第一个结点
	if(!Visit(p->data))return;
	while(p->RTag==Thread&&p->rchild!=T){
		p=p->rchild;Visit(p->data);//访问后继结，点
	}
	p=p->rchild;//p进至其右子树根
}//InOrderTraverse_Thr

三、如何建立线索链表

在中序這历过程中修改结点的左、右指针域，以保存当前访问结，点的“前驱”和“后继”信息。遍历过程中，附设指针pr,并始终保持指针pre指向当前访问的、指针p所指结点的前驱。

void InThreading(BiThrTree p){
if(p){//对以p为根的非空二叉树进行线索化
InThreading(p->lchild);//左子树线索化
if (!p->lchild)//建前驱线索
{p->LTag Thread;p->lchild pre;}
if(!pre->rchild)//建后继线索
{pre->RTag Thread;pre->rchild p;}
pre=p;
//保持pre指向p的前驱
InThreading(p->rchild);
//右子树线索化
}//if
}//InThreading

Status InOrderThreading(BiThr Tree &Thrt,BiThrTree T){//构建中序线索链表
if (!(Thrt =(BiThrTree)malloc(sizeof(BiThrNode))))
	exit (OVERFLOW);
Thrt->LTag=Link;Thrt->RTag =Thread;
Thrt->rchild=Thrt;//添加头结点
if (!T)Thrt->lchild Thrt;
else{
	Thrt->lchild T;pre Thrt;
	InThreading(T);
	pre->rchild=Thrt;//处理最后一个结点
	pre->RTag Thread;
	Thrt->rchild pre;
}
return OK
}//InOrder Threading

5.6 树和森林的表示方法

树的存储结构

1、双亲表示法：用数组存储树，每个结点保存父结点的索引。
缺点：求结点的子结点时需要遍历树。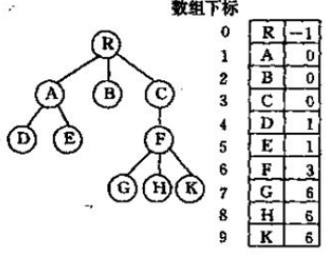

2、孩子表示法：用数组存储，数组的每个元素包含一个链表，链表中每一结点保存该元素的一个子结点索引。
缺点：不便于求结点的父结点。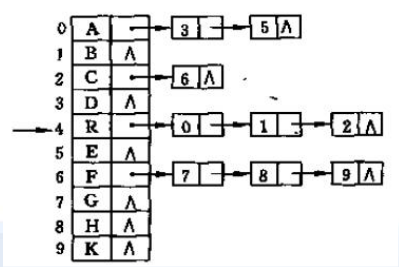

3、父子表示法结合：既存储父结点索引，又存储子结点索引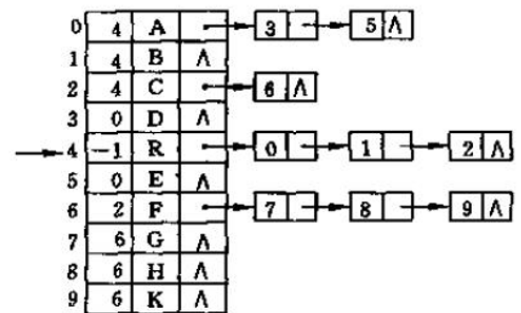

树与二叉树（二又链表）的转换

• 转换方法：
  —加线：在兄弟之间加一连线；
  —抹线：对每个结点，除了其左孩子外，去除其与其余
  孩子之间的关系。

森林与二叉树的转换（不考）

·转换方法：
一将各棵树分别转换成二叉树
一将每棵树的根结，点用线相连

5.7 赫夫曼树与赫夫曼编

最优树的定义

• 结点的路径长度定义为：从根结点到该结点的路径上分支的数目。
• 树的路径长度定义为：树中每个结点的路径长度之和。
• 树的带权路径长度定义为：树中所有叶子结点的带权路径长度之和WPL(T)=w(对所有叶子结点)
  在所有含n个叶子结点、并带相同权值的叉树中，必存在一棵其带权路径长度取最小值的树，称为“最优树”

如何构造最优树

(赫夫曼算法)以二叉树为例：
(1)根据给定的n个权值{w1,w2,wn},构造n棵二叉树的集合F={T1,T2,…,Tn},
其中每棵二叉树中均只含一个带权值为w,的根结点，其左、右子树为空树；
(2)在F中选取其根结，点的权值为最小的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和；
(3)从F中删去这两棵树，同时加入刚生成的新树；
(4)重复(2)和(3)两步，直至F中只含一棵树为止。

前缀编码

指的是，任何一个字符的编码都不是同一字符集中另一个字符的编码的前缀。

利用赫夫曼树可以构造一种不等长的二进制编码，并且构造所得的赫夫曼编码是一种最优前缀编码，即使所传电文的总长度最短。

typedef struct{
unsigned int weight;
unsigned int parent,lchild,rchild;
)HTNode,*HuffmanTree;
//动态分配数组存储赫夫曼树
typedef char**HuffmanCode;//动态分配数组存储赫夫曼编码表

---

References