数据结构第六讲课程笔记——图
nets:[[../else/数据结构]] 课程笔记
6.1 图的定义和术语
一、图的抽象数据类型
图的结构定义
图是由一个顶点集V和一个弧集R构成的数据结构。
Graph=(V,R)
其中,VR={<v,w>lv,w∈V且P(v,w)}
<v,w>表示从v到w的一条弧,并称v为弧尾,w为弧头。
谓词P(V,w)定义了弧<v,w>的意义或信息。
由于“弧”是有方向的,因此称由顶点集和孤集构成的图为有向图。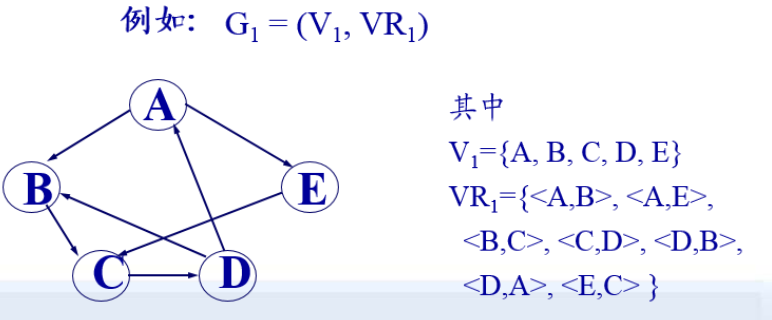
若<v,w>∈VR必有<w,v>∈VR,则称(V,w)为顶点V和顶,点w之间存在一条边。由顶点集和边集构成的图为无向图。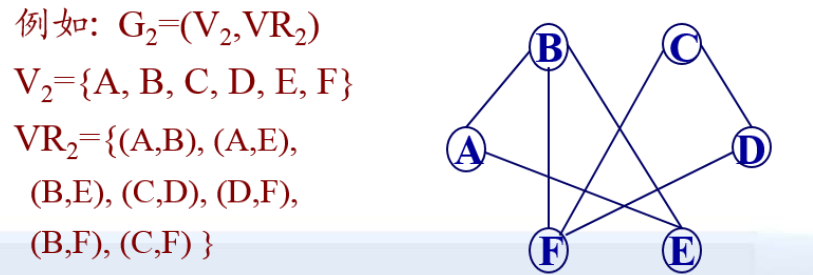
二、图的基本术语
有向网与无向网
孤或边带权的图分别称作有向网或无向网。
子图
设图G=(V,{VR})和图G’=(V’,{VR’}),且V属于’V,VR’属于VR,则称G为G的子图。
完全图/有向完全图,稀疏图/稠密图
假设图中有n个顶点,e条边,则
含有e=n(n-1)/2条边的无向图称作完全图;
含有e=n(n-1)条孤的有向图称作有向完全图;
若边或孤的个数e<nlogn,则称作稀疏图,否则称作稠密图;
邻接点、关联、度
假若顶点v和顶点w之间存在一条边,则称顶点v和w互为邻接点,边(v,w)和顶点V和w相关联。
和顶点ⅴ关联的边的数目定义为边的度。
出度/入度
顶,点的出度:以顶,点V为孤尾的孤的数目;
顶点的入度:以顶点V为孤头的孤的数目。
路径/路径长度,简单路径/简单回路
设图G=(V,{VR})中的一个顶点序列{u=vi,0,vi,1,,Vi,m=w}中,(Vi,j-1,Vi,j)属于VR,1<=j<=m,则称从顶点u到顶点w间存在一条路径。
路径上边的数目称作路径长度。
简单路径:序列中顶点不重复出现的路径。
简单回路:序列中第一个顶点和最后一个顶点相同的路
径
连通图/联通分量/强连通分量
若图G中任意两个顶,点之间都有路径相通,则称此图为连通图;
若无向图为非连通图,则图中各个极大连通子图称作此图的连通分量。
对有向图,若任意两个顶点之间都存在一条有向路径,则称此有向图为强连通图。否则,其各个强连通子图称作它的强连通分量。
生成树/森林
假设一个连通图有n个顶点和e条边,其中n-1条边和n个顶点构成一个极小连通子图,称该极小连通子图为此连通图的生成树。
对非连通图,则称由各个连通分量的生成树的集合为此非连
通图的生成森林。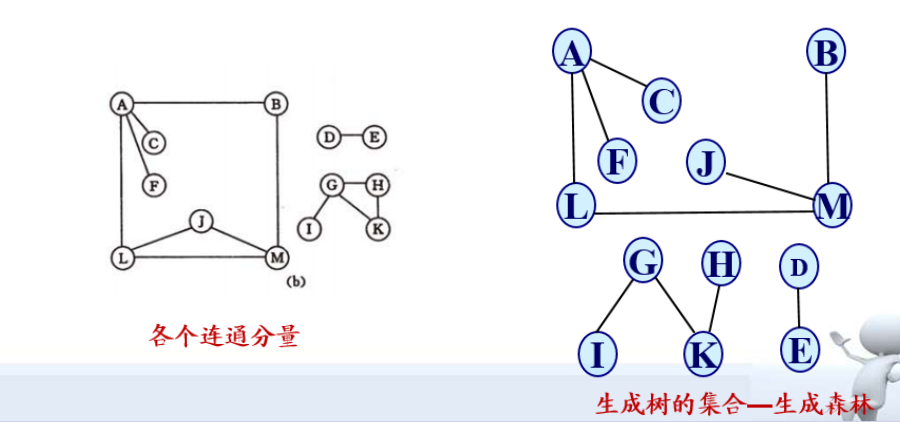
三、图的基本操作
插入或删除顶点
InsertVex(&G,v);//在图G中增添新顶点v。
Delete Vex(&G,v);∥删除G中顶点v及其相关的孤。
插入和删除孤
Insertarc(&G,V,W);
//在G中增添孤<V,w>,若G是无向的,则还增添对称孤<w,V>。
DeleteArc(&G,V,w);
//在G中删除孤<v,w>,若G是无向的,则还删除对称孤<w,V>。
遍历
DFSTraverse(G,v,Visit());
//从顶点v起深度优先遍历图G,并对每个顶,点调用函数Viisit一次且仅一次。
BFSTraverse(G,v,Visit());ii
//从顶点v起广度优先遍历图G,并对每个顶点调用函数Visiit一次且仅一次。
6.2 图的存储表示
一、图的数组(邻接矩阵)存储表示
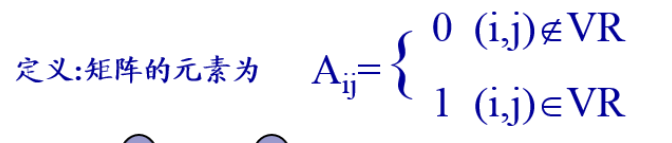
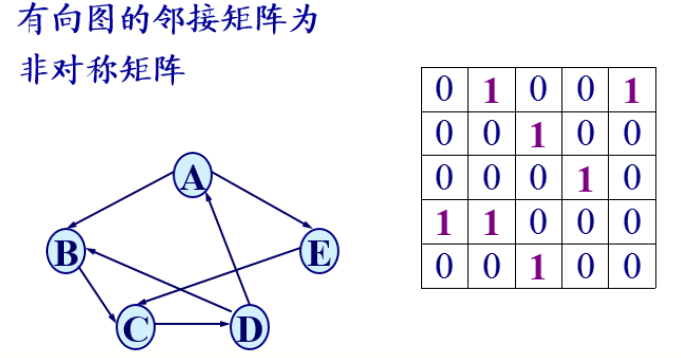
1 | typedef struct ArcCell{//孤的定义 |
二、图的邻接表存储表示
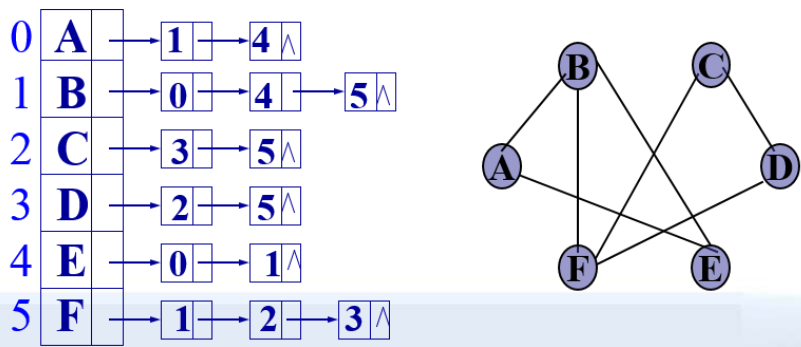
有向图的邻接表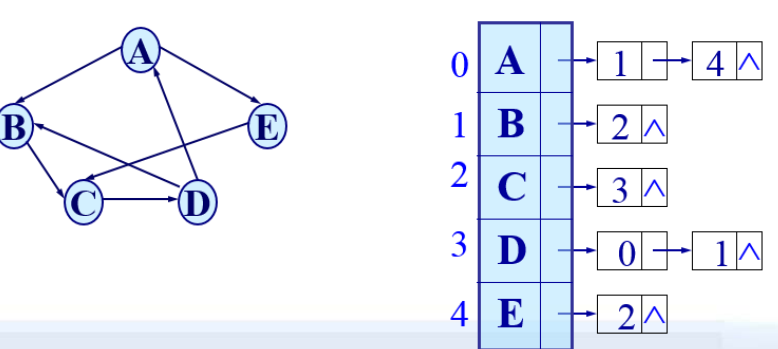
有向图的逆邻接表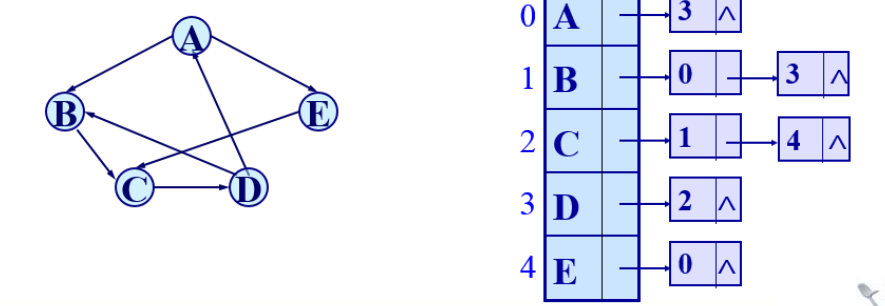
1 | typedef struct ArcNode{ |
三、有向图的十字链表存储表示
四、无向图的邻接多重表存储表示
6.3 图的遍历
深度优先遍历
连通图的深度优先搜索遍历
从图中某个顶点V出发,访问此顶点,然后依次从V的各个未被访问的邻接,点出发深度优先搜索遍历图,直至图中所有和V,有路径相通的顶点都被访问到。
深度优先搜索类似于树的先根遍历,是树的先根遍历的推广。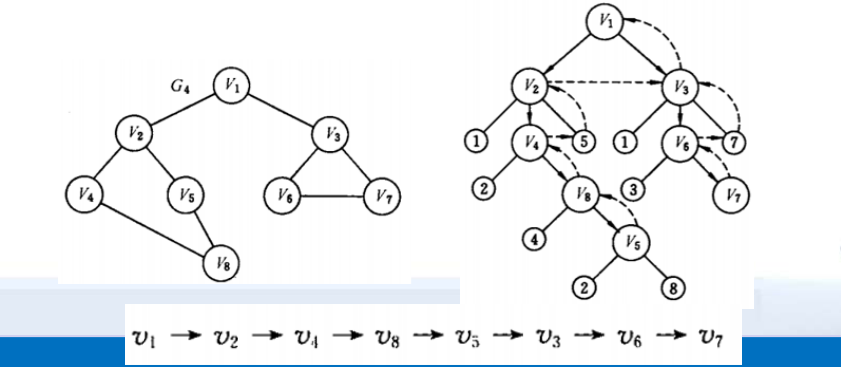
1 | void DFS(Graph G,int v){ |
非连通图的深度优先搜索遍历
首先将图中每个顶点的访问标志设为FALSE,之后搜索图中每个顶点,如果未被访问,则以该顶点为起始点,进行深度优先搜索遍历,否则继续检查下一顶点。
1 | void DFSTraverse(Graph G,Status (*Visit)(int v)){ |
广度优先遍历
从图中的某个顶点V0出发,并在访问此顶点之后依次访问V0的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和V有路径相通的顶点都被访问到。
若此时图中尚有顶,点未被访问,则另选图中一个未曾被访问的顶,点作起始点,重复上述过程,直至图中所有顶,点都被访问到为止。
类似于层次遍历
1 | void BFSTraverse(Graph G,Status (*Visit)(int v)){ |
遍历应用举例
例如:求从顶点b到顶点k的一条简单路径。
从顶点b出发进行深度优先搜索遍历。
假设找到的第一个邻接点是C,则得到的结点访问序列为:
|b c h d a e k| f g,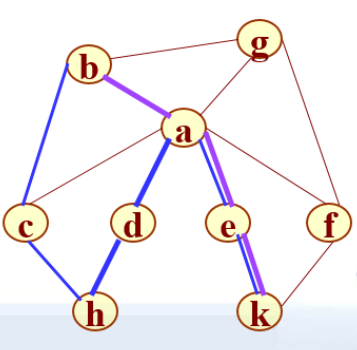
6.4 最小生成树(弱化)
构造网的一棵最小生成树,即:在e条带权的边中选取n-1条边(不构成回路),使“权值之和”为最小。
算法一:普利姆算法
取图中任意一个顶点ⅴ作为生成树的根,之后往生成树上添加新的顶点W在添加的顶点w和已经在生成树上的顶点V之间必定存在一条边,并且该边的权值在所有连通顶,点ⅴ和w之间的边中取值最小。之后继续往生成树上添加顶点,直至生成树上含有n-1个顶点为止。
一般情况下所添加的顶点应满足下列条件:
在生成树的构造过程中,图中n个顶点分属两个集合:已落
在生成树上的顶,点集和尚未落在生成树上的顶,点集V-U,则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。
算法二:克鲁斯卡尔算法
考虑问题的出发点:为使生成树上边的权值之和达到最小,则应使生成树中每一条边的权值尽可能地小。
具体做法:先构造一个只含n个顶点的子图SG,然后从权值最小的边开始,若它的添加不使SG中产生回路,则在SG上加上这条边,如此重复,直至加上n-1条边为止。

6.5 拓扑排序和关键路径
何为”拓扑排序“
对有向图进行如下操作:
按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系。由此所得的顶点的线性序列称之为拓扑排序。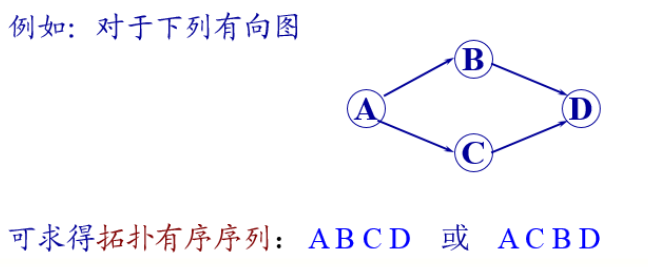
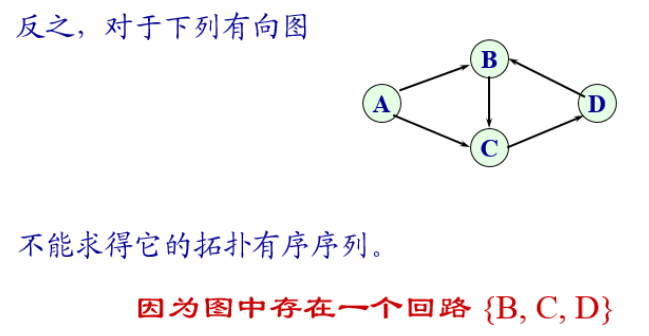
如何进行拓扑排序
一、从有向图中选取一个没有前驱的顶点,并输出之;
二、从有向图中删去此顶点以及所有以它为尾的孤;重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
6.6最短路径
单源最短路经问题
单源点路径问题是指,已知一个有向带权图中某个源点,求得从该源点到图中其它各个顶点之间的最短路径。
迪杰斯特拉算法思想
如果从源点到某个终点存在路径,必存在一条路径长度取最小值的路径。
迪杰斯特拉提出了一个“按各条最短路径长度递增的次序”产生最短路径的算法。该算法是基于贪心算法的。
迪杰斯特拉算法
设置辅功数组Dist,其中每个分量Dist[k]表示当前所求得的从源点到其余各顶点k的最短路径。n——图G中的顶点数。
dist[n] ——存放从源点到每个终点当前最短路径的长度。
path[n]——存放相应路径。
S——求得的最短路径的终点的集合。
- 令S={Vs},Vs为源点。并设定dist[i]的初始值。
- 选择顶点Vj使得dist[j]=Min{dist[k]I Vk属于V-S},并将顶点Vj并入到集合S中
- 对集合V-S中所有顶点Vk,若存在从V;指向该顶点的孤,且dist[j]+wk<dist[k],则修改dist[j]和path[k]的值。
- 重复[2]和[3]直至求得从源点到所有其它顶,点的最短路径为止。
一般情况下:
Dist[k]=<源点到顶点k的孤上的权值>
或者=<源点到其它顶点的路径长度>+<其它顶点到顶点k的弧上的权值>。时间复杂度O(n3)
任意两点之间的最短路径
如果希望求得图中任意两个顶,点之间的最短路径,显然只要依次将每个顶,点设为源点,调用迪杰斯特拉算法次便可求出,其时间复杂度为O(n3)。弗洛伊德(Floyd)提出了另外一个算法,虽然其时间复杂度也是O(n3),但算法形式更简单。
